Алгебраические фракталы

Это самая крупная группа фракталов. Получают их с помощью нелинейных процессов в n-мерных пространствах. Наиболее изучены двухмерные процессы. Интерпретируя нелинейный итерационный процесс, как дискретную динамическую систему, можно пользоваться терминологией теории этих систем: фазовый портрет, установившийся процесс, аттрактор и т.д. Известно, что нелинейные динамические системы обладают несколькими устойчивыми состояниями. То состояние, в котором оказалась динамическая система после некоторого числа итераций, зависит от ее начального состояния. Поэтому каждое устойчивое состояние (или как говорят - аттрактор) обладает некоторой областью начальных состояний, из которых система обязательно попадет в рассматриваемые конечные состояния. Таким образом фазовое пространство системы разбивается на области притяжения аттракторов. Если фазовым является двухмерное пространство, то окрашивая области притяжения различными цветами, можно получить цветовой фазовый портрет этой системы (итерационного процесса). Меняя алгоритм выбора цвета, можно получить сложные фрактальные картины с причудливыми многоцветными узорами. Неожиданностью для математиков стала возможность с помощью примитивных алгоритмов порождать очень сложные нетривиальные структуры.

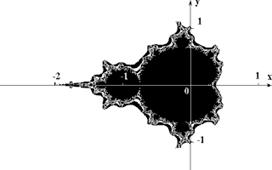
Рис. 12. Множество Мандельброта.

В качестве примера рассмотрим множество Мандельброта (см. рис.10 и рис.11). Алгоритм его построения достаточно прост и основан на простом итеративном выражении:

Z[i+1] = Z[i] * Z[i] + C(15)

где Zi и C - комплексные переменные. Итерации выполняются для каждой стартовой точки C прямоугольной или квадратной области - подмножестве комплексной плоскости. Итерационный процесс продолжается до тех пор, пока Z[i] не выйдет за пределы окружности радиуса 2, центр которой лежит в точке (0,0), (это означает, что аттрактор динамической системы находится в бесконечности), или после достаточно большого числа итераций (например 200-500) Z[i] сойдется к какой-нибудь точке окружности. В зависимости от количества итераций, в течении которых Z[i] оставалась внутри окружности, можно установить цвет точки C (если Z[i] остается внутри окружности в течение достаточно большого количества итераций, итерационный процесс прекращается и эта точка растра окрашивается в черный цвет).

Рис. 13. Участок границы множества Мандельброта, увеличенный в 200pаз.

Вышеописанный алгоритм дает приближение к так называемому множеству Мандельброта. Множеству Мандельброта принадлежат точки, которые в течение бесконечного числа итераций не уходят в бесконечность (точки, имеющие черный цвет). Точки, принадлежащие границе множества (именно там возникает сложные структуры) уходят в бесконечность за конечное число итераций, а точки лежащие за пределами множества, уходят в бесконечность через несколько итераций (белый фон).

Примеры алгебраических фракталов:

множество Мандельброта;

множество Жюлиа;

бассейны Ньютона;

биоморфы.

Похожие статьи:

Виды конфликтов в педагогическом процессе и способы их разрешения
Конфликтное взаимодействие понимается как реализация участниками конфликтной ситуации своих антагонистических позиций. При этом их действия, связанные с достижением своих целей, тормозят решение задач противников. Как показывают наблюдения, отношение педагогов к межличностным конфликтам и их действия в ситуациях конфликтного взаимодействия неоднозначны. Так, педагоги с авторитарным стилем общения ...

Формирование естественно-научных представлений у детей дошкольного возраста средствами графического моделирования
Многие известные педагоги и философы обращали внимание и необходимость открыть ребенку книгу природы как можно раньше. Это Я.А. Коменский, Ж.Ж. Руссо, И.Г. Песталоцци, К.Д. Ушинский, Л.Н. Толстой, В.А. Сухомлинский и др. Особую роль природы в развитии мышления подчеркивал К.Д. Ушинский. Он считал логику природы самой доступной, наглядной и полезной для ребенка. Именно непосредственные наблюдения ...