Геометрические фракталы

Фракталы этого класса самые наглядные. В двухмерном случае их получают с помощью некоторой ломаной (или поверхности в трехмерном случае), называемой генератором. За один шаг алгоритма каждый из отрезков, составляющих ломаную, заменяется на ломаную-генератор, в соответствующем масштабе. В результате бесконечного повторения этой процедуры, получается геометрический фрактал.

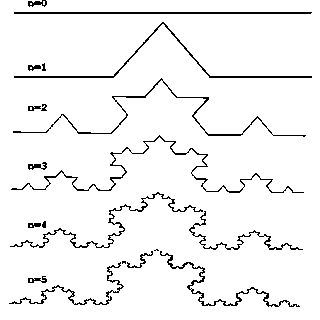
Рис. 7. Построение триадной кривой Кох.

Рассмотрим один из таких фрактальных объектов - триадную кривую Кох. Построение кривой начинается с отрезка единичной длины (рис.1) - это 0-е поколение кривой Кох. Далее каждое звено (в нулевом поколении один отрезок) заменяется на образующий элемент, обозначенный на рис. 1 через n=1. В результате такой замены получается следующее поколение кривой Кох. В 1-ом поколении - это кривая из четырех прямолинейных звеньев, каждое длиной по 1/3. Для получения 3-го поколения проделываются те же действия - каждое звено заменяется на уменьшенный образующий элемент. Итак, для получения каждого последующего поколения, все звенья предыдущего поколения необходимо заменить уменьшенным образующим элементом. Кривая n-го поколения при любом конечном n называется предфракталом. На рис.1 представлены пять поколений кривой. При n стремящемся к бесконечности кривая Кох становится фрактальным объектом.

Для построения снежинки Коха выполним следующие операции (см. рис. 8). Рассмотрим в качестве нулевой итерации равносторонний треугольник.

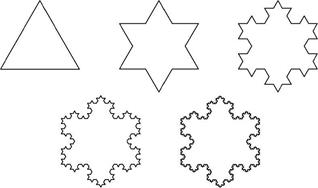
Рис. 8. Снежинка Коха.

Затем каждую из сторон этого треугольника разделим на три равные части, уберем среднюю часть и в середине достроим равносторонний треугольник так, как изображено на рис. 8. На следующем шаге такой же процедуре деления на три равные части и достраивания равностороннего треугольника подвергается каждая из сторон новой фигуры, и так до бесконечности. В результате возникает симметричная, похожая на снежинку, бесконечно изломанная кривая , которая представляет собой самоподобное множество, называемое снежинкой Коха. Отличительной ее особенностью является то, что она, будучи замкнутой, тем не менее нигде себя не пересекает, поскольку достраиваемые треугольники каждый раз достаточно малы и никогда не "сталкиваются" друг с другом.

Для получения другого фрактального объекта нужно изменить правила построения. Пусть образующим элементом будут два равных отрезка, соединенных под прямым углом. В нулевом поколении заменим единичный отрезок на этот образующий элемент так, чтобы угол был сверху. Можно сказать, что при такой замене происходит смещение середины звена. При построении следующих поколений выполняется правило: самое первое слева звено заменяется на образующий элемент так, чтобы середина звена смещалась влево от направления движения, а при замене следующих звеньев, направления смещения середин отрезков должны чередоваться. На рис.9 представлены несколько первых поколений и 11-е поколение кривой, построенной по вышеописанному принципу. Предельная фрактальная кривая (при n стремящемся к бесконечности) называется драконом Хартера-Хейтуэя.

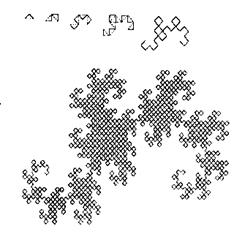
Рис. 9. Построение "дракона" Хартера-Хейтуэя .

К геометрическим фракталам также относят фракталы, получаемые похожими процедурами, например:

множество Кантора;

треугольник Серпиньского;

коврик Серпиньского;

кладбище Серпиньского;

губка Менгера;

дерево Пифагора.

В машинной графике использование геометрических фракталов необходимо при получении изображений деревьев, кустов, береговой линии. Двухмерные геометрические фракталы используются для создания объемных текстур (рисунка на поверхности объекта) .

Похожие статьи:

Роль досугов в обучении детей старшего возраста двигательным умениям и навыкам
Известно, что в результате учебной деятельности, связанной с длительным поддержанием статической позы у детей развивается утомление, падает активность, внимание, понижается восприятие. Выполнение физических упражнений вызывает активную работу мышц, а это в свою очередь усиливает кровообращение и тем самым повышает интенсивность работы сердца, активизирует деятельность нервной системы, повышает то ...

Анализ опыта преподавателей по исследуемой работе
С целью изучения опыта преподавателей по использованию рифмовок и стихотворений я посетила уроки английского языка в 6 классах СОШ №2. Преподаватели используют рифмовочные и стихотворные приёмы обучения в этой школе практически на каждом уроке английского языка. Учитель уделяет большое внимание отбору стихотворений, в основу которых положены принципы: тематический, познавательный и дидактический. ...