Триадное канторовское множество

Канторовские множества позволяют проиллюстрировать достаточно много важных и интересных специфических особенностей, присущих фракталам.

Очень простое построение, предложенное Кантором, позволяет получать фрактальные множества с фрактальной размерностью в интервале 0<D<1. Как показано на рис. 10, затравкой служит единичный отрезок [0, 1], а образующий элемент делит его на три равные части и отбрасывает открытую среднюю часть, оставляя ее концевые точки. Затем образующий элемент применяется к каждому из двух оставшихся подынтервалов и т. д. Такая процедура очень быстро приводит к очень коротким отрезкам. Поскольку наша графика имеет конечное разрешение, мы обнаруживаем, что 6-е поколение отрезков неотличимо от 5-го. После бесконечного числа поколений оставшееся бесконечное множество точек рассеяно по единичному отрезку. Это множество называется канторовской пылью.

Вычислим теперь для канторовского множества различные размерности, введенные нами в предыдущих разделах.

Начнем с размерности Хаусдорфа-Безиковича, определяемой выражением (2.3). В n-м поколении канторовское множество состоит из N=2n отрезков длиной li = (1/3)n, i=1, 2, .,N. Если попытаться покрыть множество прямолинейными отрезками длины δ=li и расположить их аккуратно, то нам удастся покрыть все отрезки п-го поколения и, следовательно, все точки канторовского множества. Мера, определяемая формулой (2.3), равна величине

(11)

Рис. 10. Построение Триадного канторовского множества. Затравка-единичный отрезок [0,1]. Образующий элемент удаляет среднюю треть. На рисунке показаны первые пять поколений. D = ln2/ln3 = 0,6309.

Эта мера расходится или стремится к нулю при δ→ 0, если только мы не выберем d= D = ln2/ln3 = 0,6309. Топологическая размерность канторовского множества определяется величиной DT = 0. Так как DT < D, мы заключаем, что Триадное канторовское множество есть фрактальное множество с фрактальной размерностью

(12)

Описываемое здесь канторовское множество не вполне самопо-добно. Однако мы можем расширить его с помощью процедуры экстраполяции, охватывающей область двумя канторовскими множествами, которые покрывают интервалы. Повторяя этот процесс неограниченное число раз, мы можем построить самоподобное множество на полупрямой [0, ∞]. Если изменить масштаб в r = 1/3 раза, то, чтобы покрыть исходное множество, нам понадобится N — 2 таких множеств. Из определения размерности подобия Ds получаем

(13)

Размерность подобия совпадает с фрактальной размерностью Триадного канторовского множества.

Формула (13) позволяет тривиальным образом построить канторовское множество с любой заданной размерностью из интервала 0 < D < 1. В качестве примера на рис. 11 показаны два различных построения, которые оба приводят к одной и той же размерности D = 1/2. Внешне два множества "выглядят" по-разному, хотя они оба имеют одну и ту же фрактальную размерность: у них различная лакунарность.

Размерность кластера, или размерность массы, мы получим, если рассмотрим экстраполированный вариант канторовского множества. Начнем с "мономеров" длиной R0 и образуем "кластер" из N = 2 мономеров длиной R=3R0, после чего все повторим сначала, приняв димер за новый исходный мономер, и т.д. Кластер из N = 2n мономеров имеет диаметр R = 3n. Следовательно, фрактальная размерность этого кластера, определяемая соотношением (13), равна

(14)

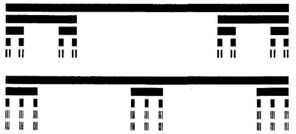
Рис. 11. Два построения канторовского множества с D = 1/2. Вверху: N = 2 и r = 1/4; внизу: N = 3 и r = 1/9.

Размерность кластера совпадает с фрактальной размерностью этого канторовского множества.

Мы заключаем, что для весьма простого Триадного канторовского множества все определенные выше различные размерности совпадают.

Похожие статьи:

Особенности развития воображения в дошкольном возрасте
Особенности развития детей старшего дошкольного возраста, прежде всего, проявляются в интенсивном развитии мышления и других интеллектуальных процессов, существенном изменении мотивационной сферы, ориентации на социальные отношения в мире взрослых. Многие психологи считают, что именно в этом возрасте проблема развития воображения должна вставать на первые планы в воспитании ребёнка. Носителем соц ...

Результаты реализации готовности студентов к воспитательной деятельности с трудными подростками
На первом этапе работы участники экспериментальной группы изучали учащихся. Использовались методы: анкетирование, устный опрос, собеседование, тестирование двигательной подготовленности, изучение школьной, медицинской документации, определение уровня тревожности, психологического климата в классном коллективе, мотивов участия в деятельности, отношений в семье. Просмотр психолого-педагогических ха ...