Размерность фрактала

Для отрезка прямой линии длиной L (состоящего из бесконечного числа точек) минимальное число N(l) одномерных отрезков размера l, с помощью которых можно покрыть данный отрезок целиком, равно, очевидно, N(l) = L/l. В этом случае, согласно формуле (17) (или (16)), фрактальная размерность D = 1, т.е. совпадает с Евклидовой размерностью отрезка прямой d = 1. Для области площадью S гладкой двумерной поверхности число необходимых для ее покрытия квадратиков N(l) = S/l2 (при достаточно малых l), поэтому фрактальная размерность гладкой поверхности D = 2. И наконец, для покрытия некоторого конечного объема V необходимо N(l) = V/l3 кубиков с ребром l. Следовательно, фрактальная размерность этого множества D = 3.

Разберем теперь некоторые классические примеры регулярных фракталов, которые обладают свойством идеального самоподобия. Их покрытие можно осуществлять элементами, из которых состоит данный фрактал. В этом случае имеет место упрощенный вариант формулы (17) для определения фрактальной размерности. Пусть на некотором этапе покрытия фрактала нам пришлось использовать, как минимум, N(l) таких элементов характерного размера l, а на другом N(l') элементов размера l'. Тогда величина фрактальной размерности D может быть вычислена по формуле:

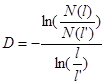(18)

Очевидно, эту формулу можно переписать в виде:

(19)

что является следствием выражения (16).

Похожие статьи:

Эксперимент сравнения итогов усвоения материала на традиционных уроках и иновавционных с применением игровых технологий
Качество образования определяется не только количеством и качеством знаний, но и качеством личностного, духовного, гражданского развития подрастающих поколений. И именно в этом его главная общественная ценность. Исследование включает в себя сравнения качества усвоения материала на традиционных и инновационных с применением игровых технологий. Эксперимент был проведён на базе Мышленской общеобразо ...

Характеристика и сущность изучения развития физических качеств
В процессе физического воспитания детей дошкольного возраста необходимо решать образовательные задачи: формирование двигательных навыков и умений, развитие двигательных и физических качеств, привитие навыков правильной осанки, навыков гигиены, освоение специальных знаний. Благодаря пластичности нервной системы двигательные навыки и умения формируются у детей сравнительно легко. Большинство движен ...