Анализ учебной литературы по теме «Обыкновенные дроби и проценты»

Изучение обыкновенных дробей и процентов начинается в 5 классе и продолжается на протяжении всего курса алгебры. Начиная с 6 класса, знания о дробях и процентах обобщаются, расширяются и систематизируются.

И, следовательно, анализ учебной литературы необходимо проводить за 5-6 классы, чтобы на основе этого анализа построить содержание дидактического пособия. Цель нашего пособия состоит в визуализации базовых понятий, лежащих в основе тем «обыкновенные дроби» и «проценты». Поэтому, в первую очередь, обратим внимание на визуальные задачи, способствующие формированию этих понятий. При анализе учебных пособий будем применять классификацию визуальных задач, предложенную Н.А. Резник.

Тема «Обыкновенные дроби» в данном учебном пособии изложена в главе II «Дробные числа». Учащиеся 5 класса знакомятся с простейшими дробями: ; ; … Образование долей происходит на наглядной основе. Происхождение дробей разбирается как результат деления на любое число равных частей.

Например:

Мама купила арбуз и разрезала его на 6 равных частей: бабушке дедушке, папе, двум детям и себе. Эти равные части называют долями.

Так как арбуз разрезали на 6 долей, то каждый получит «одну шестую долю арбуза», или короче, «одну шестую арбуза».

Затем вводится определение обыкновенной дроби, где выделяют числитель и знаменатель, делая акцент на соотношении взятых долей к количеству долей, на которое делят целое. Записи вида называют обыкновенными дробями. В дроби число 5 называют числителем дроби, а число 8 – знаменателем дроби. Знаменатель показывает, на сколько долей делят, а числитель – сколько таких долей взято.

Образование дробей, как и образование долей рассматривается с помощью наглядных примеров.

После ряда обучающих визуальных задач типа «посмотрите и найдите», например:

№884. Какая часть фигуры закрашена?

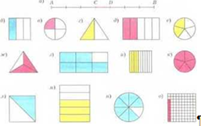
Предложены задачи на дроби, включенные в рассмотрение этого пункта 23 «Доли. Обыкновенные дроби». Выделяют три типа задач: задачи на доли; нахождение части от числа; нахождение числа по его части. Сначала решаются задачи и примеры на нахождение одной части от числа (числа по его части): ; и т. п.

Например:

№889. Купили кусок ткани длиной 2 м 50 см и из куска сшили платье для куклы. Сколько сантиметров ткани ушло на это платье?

№891. Петя готовил уроки 1 ч 40 мин. На математику он потратил этого времени, а на историю – оставшегося времени. Сколько минут Петя готовил уроки по математике и сколько по истории?

Дальше переходят к задачам и примерам на отыскание нескольких частей целого. Дается задача – математическая модель, на основе которой рассматриваются все три типа задач. Каждая из задач имеет иллюстративное приложение и решение, описанное в учебнике.

Похожие статьи:

Особенности формирования ценностного отношения к профессиональной деятельности у будущих учителей
Важным показателем успешности профессионального становления будущего педагога является сформированность его ценностно-смысловой сферы. Так Н.Н. Никитина отметает важность выдвижения на передний план аксиологического подхода к подготовке учителя, согласно которому педагогическое образование должно обеспечить не только усвоение профессиональных знаний и умений, но и развить его ценностное сознание, ...

Методы работы по орфографии в школе
Термин «орфография» создан на базе корней греческих слов orthos (правильный) и grapho (пишу); буквальным переводом (калькой) его на русский язык является термин «правописание» . В современном понимании орфография – это система правил написания слов. Правила эти не однотипны, поэтому и в самой орфографии выделяется несколько относительно самостоятельных частей. Орфография, как система правил, сост ...