Анализ учебной литературы по теме «Обыкновенные дроби и проценты»

Далее рассматриваются аналогичные задачи, затем вводится определение: Частное от деления натуральных чисел m и n можно записать в виде дроби , где m – числитель, а n – знаменатель:

.

Затем дробь рассматривается как количество равных долей. Представлена визуальная задача типа «проверь себя»:

№332. Кусок проволоки длиной 2 м разрезали на 3 равные части. Какова длина одной части?

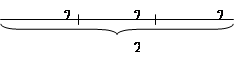
Проверьте, так ли вы рассуждали при решении этой задачи.

Чтобы найти длину одной части, надо длину всего куска разделить на число частей: 2 : 3.

Частное удобно записывать в виде дроби: .

Решение: 2 м : 3 = м.

Ответ: длина одной части – м.

Далее следует ряд заданий, отмеченных знаком «У», выполняя которые ученики узнают что-нибудь новое (правило, свойство уже известного понятия).

№338 (У).

Ленту длиной 1 м разрезали пополам, а ленту длиной 2 м разрезали на 4 части. Какова длина одной части в каждом случае (в метрах)?

Сделайте рисунок к задаче, изобразив ленты в виде прямоугольников шириной 5 мм, а длиной, соответственно, 4 и 8 см. Выполните задания:

Сравните отрезки длиной м и м;

Сравните дроби и .

«Проверьте себя».

Если вы все сделали правильно, то у вас должны получиться такие рисунки:

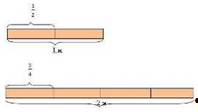
Из рисунков видно, что =

Таким образом, учащиеся знакомятся с интересным и важным свойством дробей: «одну и ту же дробь можно записывать несколькими способами». Здесь не приводится формулировка основного свойства, подробное изучение вынесено в отдельный параграф 21 «Основное свойство дроби». Перед этим разбирается вопрос о происхождении дробей, как одна или несколько равных долей:

Чтобы получить дробь , надо единицу разделить на n равных частей и взять m таких частей.

Чтобы получить дробь , надо число m разделить на число n.

Представлен ряд обучающих визуальных задач:

№341 («Посмотрите и найдите»).

а) В семье четверо детей – одна девочка и трое мальчиков. Праздничный торт был разрезан на 6 одинаковых кусков: по одному на каждого ребенка и на каждого из родителей. Какая часть торта досталась девочке, а какая – мальчикам (рис. 36)?

б) Участок площадью 1 а был поделен на 10 грядок. На двух грядках был посажен лук, на трех – свекла, на четырех – морковь и на одной – чеснок. Найдите площадь (в арах) под каждой из этих овощных культур (рис. 37).

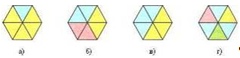
№342 («Тренажер»). Запишите в виде дроби, какая часть фигуры закрашена голубым цветом:

Похожие статьи:

Наука как важнейшая функциональная часть общества
Сейчас наука стала неотъемлемой частью нашей повседневной жизни и культуры. Даже большинство ученых о новейших достижениях в своей собственной области из последних номеров ежедневных газет и выпусков теленовостей. В современном мире наука - такая же обычная сфера человеческой деятельности, как торговля, промышленное производство и сельское хозяйство, а профессия ученого стала одной из массовых пр ...

Экологическое воспитание младших школьников
Глобальные проблемы современности, несущие угрозу жизни и человеческой цивилизации, вызвали необходимость экологического образования, призванного реализовать идеи становящегося экологически информационного общества. Поиск путей гармонического взаимодействия общества и природы приводит к интенсивному процессу экологизации общей культуры человечества, и как следствие, - к формированию теории и прак ...