Анализ учебной литературы по теме «Обыкновенные дроби и проценты»

Решение:

Таким образом, учащиеся могут сравнить две решаемые задачи, после чего сделать вывод: 1) чтобы найти часть от целого, надо число, соответствующее целому разделить на знаменатель и результата умножить на числитель дроби, которая выражает эту часть; 2) чтобы найти целое по его части, надо число, соответствующее этой части, разделить на числитель и результат умножить на знаменатель дроби, которая выражает эту часть.

Заметим, что прежде чем приступать к решению таких задач авторы просят ответить на вспомогательные вопросы:

что принято за целое?

известна ли эта величина?

что теребуется найти в задаче: часть от целого или целое по его части?

как найти величину, которая приходится на одну часть?

Система упражнений выстроена от простого к сложному, где задания сложнее отмечены специальным значком «о»:

№367 (о) («Серия»). Сделайте в тетради такой же рисунок и закрасьте указанную часть соответствующей фигуры:

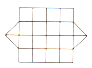
а) ; б) ; в) .

№396. Запишите, какая часть фигуры закрашена:

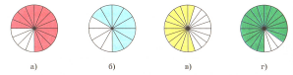
Основное свойство дроби выводится из рассмотрения примеров на увеличение или уменьшение величины дроби в связи с увеличением и уменьшением ее членов в несколько раз. Рассмотрение примеров иллюстрируется чертежом, на котором учащиеся проверяют, что равные дроби могут быть выражены в различных видах.

№371 (У) («Серия»). Запишите, какая часть фигуры закрашена оранжевым, какая – желтым и какая – зеленым цветом. Постарайтесь найти разные способы.

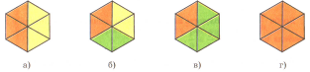
№372 (У) («Серия»). Запишите, какая часть фигуры закрашена, а какая – не закрашена. Найдите разные способы.

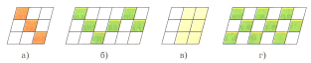
№390 (о) («Серия»). Запишите, какая часть фигуры закрашена:

После решения примеров делаются выводы: величина дроби не изменится, если числитель и знаменатель увеличить в одинаковое число раз; величина дроби не изменится, если числитель и знаменатель уменьшить в одинаковое число раз. Основное свойство представлено символьной записью:

При изучении сокращения дробей авторы добиваются, чтобы учащиеся поняли а) на каком свойстве дробей основано их сокращение; б) цель этого преобразования (вид дроби упрощается, так как числитель и знаменатель выражаются меньшими числами). Осуществляется это с помощью вспомогательных вопросов: Какое свойство дроби для этого можно использовать? После чего авторы предлагают прочитать рубрику «Проверь себя». Здесь же проводится сравнение дробей, опираясь на основное свойство дроби.

Похожие статьи:

Анализ опытно – экспериментальной работы
Экспериментальная база нашего исследования – ДОУ № 17 г. Армавира Краснодарского края. Экспериментальная группа – дети старшего дошкольного возраста с замедленным психическим развитием: Испытуемый № 1 : Беляко Данил 5 лет 11 мес. Испытуемый № 2: Корташёв Руслан 6 лет 1 мес. Испытуемый № 3: Иванов Данил 5 лет 7 мес. Испытуемый № 4: Корх Андрей 6 лет Испытуемый № 5: Пипеляев Дима 5 лет 9 мес. Экспе ...

Особенности формирования двигательных навыков и умений детей старшего дошкольного возраста, имеющих отклонения в развитии
Дошкольный возраст является периодом интенсивного формирования всех органов и систем организма и сензитивным периодом психического развития. Именно в дошкольном детстве развивающего развиваются те двигательные качества, навыки и умения ребенка, которые служат основой его нормального физического и психического развития. Движения - основа здорового состояния организма человека, без них невозможна е ...