Анализ учебной литературы по теме «Обыкновенные дроби и проценты»

Класс визуальных задач «Посмотри и найди»:

№17. Какую часть отрезка АВ составляет отрезок CD? Какую часть отрезка CD составляет отрезок АВ?

№18. Какую часть каждый из отрезков АВ, CD и EF составляет от других отрезков? Сделай записи.

Авторы «приучают» детей сознательно разбираться в особенностях дробей, чтобы использовать эти свойства в различных преобразованиях.

Глава 3, § 1, п. 2. «Основное свойство дроби. Преобразование дробей». Основное свойство дроби выводится из рассмотрения примеров на увеличение или уменьшение величины дроби в связи с увеличением и уменьшением ее челнов в несколько раз. Рассмотрение примеров иллюстрируется чертежом.

= , числитель и знаменатель второй дроби в 5 раз превышает числитель и знаменатель первой дроби. Вывод из рассуждений записывают в виде правила, основного свойства дроби: Если числитель и знаменатель дроби умножить или разделить на одно и то же натуральное число, то получится равная ей дробь:

Приводится замечание: основное свойство дроби показывает, что всякое целое или дробное число можно записать в виде дроби бесконечным числом способов, например:

3 = = = = = …

Выделяют обучающие визуальные задачи «Посмотри и определи»:

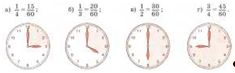
№60. Объясните равенство дробей сначала с помощью рисунка, а потом с помощью основного свойства дроби:

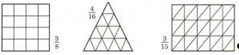
№115. Перерисуйте фигуры в тетрадь. Закрасьте части фигур, соответствующие указанным дробям. Какими еще дробями можно выразить закрашенные части фигур? Запиши ответ с помощью равенств.

Опираясь на основное свойство дроби, авторы отмечают, что всегда можно добиться, чтобы дроби имели или один и тот же знаменатель, или один и тот же числитель, что затем их можно было сравнить. Правило сравнение дробей очевидно из самого понятия дроби: ясно, если мы делим какую-то сумму денег на несколько равных частей, то чем больше мы возьмем таких частей, тем больше денег нам достанется; если делим предмет на большее число частей, то каждая часть получается меньше. Отсюда правила:

из двух дробей с одинаковыми знаменателями меньше та дробь, у которой числитель меньше;

из двух дробей с одинаковыми числителями меньше та дробь, у которой знаменатель больше.

В качестве специального вопроса рассматриваются примеры решения задач на нахождение части целого и целого по его части.

Выделяют три задачи:

Задачи на нахождение части от числа, выраженной дробью.

Задачи на нахождение числа по его части, выраженной дробью.

Задачи на нахождение дроби, которую одно число составляет от другого.

Тип задачи определяется тем, что неизвестно – a, b или , где а – некоторая величина, принятая за единицу («целое»), b – некоторая часть целого, выраженная дробью .

Похожие статьи:

Эффективность организационно-содержательного обеспечения процесса формирования готовности к работе с трудными подростками
Экспериментальная работа организовывалась и проводилась в 2 этапа. Первый этап был связан с формированием готовности студентов к воспитательной работе с трудными подростками в процессе профессиональной подготовки будущих специалистов в сфере физической культуры. На данном этапе реализовывался разработанный нами спецкурс (содержание и объем представлены в главе 2, параграфе 2.2.). В эксперименте п ...

Формирование темповой организации высказывания
Логопедическая работа по развитию у дошкольников с ЗПР способности использовать в речи различные темповые характеристики осуществляется в три этапа: 1. Развитие общих представлений о темпе речи. 2. Развитие восприятия различного темпа речи. Выделение данного этапа обусловлено прежде всего тем, что достаточный уровень развития речевого слуха и, в частности, таких его компонентов, как восприятие и ...