Анализ учебной литературы по теме «Обыкновенные дроби и проценты»

Закрепить основное свойство предлагается примерами:

№761. Объясните с помощью рисунка, почему = = = .

При вычислениях с дробями допускается сокращение дроби на любой общий делитель ее числителя и знаменателя (необязательно наибольший), а также приведение дробей к любому общему знаменателю (необязательно к наименьшему). Но в этом и в другом случае разъясняется, когда вычисления будут наиболее рациональными.

Формирование понятия дроби сопровождается обучением решению простейших задач на нахождение части числа и числа по его части. В пункте 4.3 «Нахождение части числа и числа по его части» соответственно рассматриваются только две задачи:

Задача 1. Было 1000 рублей, этой сумы истратили. Сколько денег истратили?

Решение. Будем считать, что 1000 р. Состоит из пяти пятых долей. Тогда на одну пятую приходится 1000 : 5 = 200 р., а на две пятых – в два раза больше: 200 · 2 = 400 р. Эти два действия можно объединить: 1000 : 5 · 2 = 400 р.

Чтобы найти числа 1000, можно это число разделить на знаменатель дроби и результат умножить на числитель.

Задача 2. Потратили 600 рублей, что составило имевшейся суммы денег. Сколько было денег?

Решение. Будем считать, что искомое число состоит из трех третьих долей. По условию его две трети равны 600. Тогда на одну треть приходится 600 : 2 = 300 р., а на три трети 300 · 3 = 900 р. Эти два действия можно объединить: 600 : 2 · 3 = 900 р.

Чтобы найти число, которого равны 600, можно 600 разделить на числитель дроби и результат умножить на знаменатель.

После приведения дробей к общему знаменателю появляется потребность в сравнении дробей. Сравнение осуществляется при помощи чертежа.

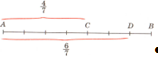
Из двух дробей с общим знаменателем больше та дробь, у которой числитель больше. Вводятся обозначения: если p > r, то > .

Здесь же авторы вводят определение правильной и неправильной дробей. Доказывается следующее утверждение: если первая дробь меньше второй, а вторая дробь меньше третьей, то первая дробь меньше третьей.

После чего приводятся примеры для решения.

№807. Сравните правильную и неправильную дроби:

а) с 1; б) между собой.

№808. С помощью рисунка объясните, почему > , < .

Смешанная дробь рассматривается как другая запись обыкновенной неправильной дроби.

Заключительный этап изучения темы – изображение дробей точками на координатной прямой.

В данной теме решаются задачи на умножение и деление дробей, а также обращается особое внимание на то, что рассмотренные ранее задачи на дроби можно решать с помощью умножения и деления на дробь.

Похожие статьи:

Приемы формирования знаний и умений по обогащению английского вокабуляра с применением коммуникативного подхода
Коммуникативный подход - это «стратегия, моделирующая общение, направленная на создание психологической и языковой готовности к общению, на сознательное осмысление материала и способов действий с ним, а так же на осознание требований к эффективности высказывания». Основным же критерием, позволяющим отличить этот подход от других видов учебной деятельности, является то, что учащиеся самостоятельно ...

Организация коррекционно-развивающей работы с обучающимися с особыми образовательными потребностями
По мнению Лисиной и Ломова психическое развитие и формирование личности ребенка возможно только в процессе общения со взрослым, а также по мнению Д.Б. Эльконина с опорой на ведущий вид деятельности ребенка. Так как развитие аномального ребенка происходит по тем же законам, что и развитие нормального ребенка, то при создании определенных условий все дети обладают способностью к развитию (Л.С. Выго ...