Методические основы изучения тем «Обыкновенные дроби и проценты» в школе

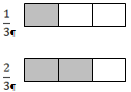
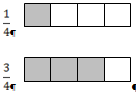
Дальше переходим к задачам на отыскание нескольких частей от целого: «Скорость полета стрижа 1600 м в минуту, скворца и ястреба скорости полета стрижа. Найти скорость полета скворца и ястреба в минуту».

Решение: Надо найти , от числа 1600 м. Начинать решение целесообразно со следующих вопросов:

Сколько четвертых частей числа можем (умеем) найти? (.)

Как это сделать? (1600 разделить на 4 равные части.)

Сколько получится? (1600 : 4 = 400 м.)

Как найти от числа 1600 м? (Надо 400 м умножить на 3.)

Почему? ( больше в 3 раза.)

Сколько получится? (400 ∙ 3 = 1200 м.)

Что показывает число 1200 м? (Скорость полета скворца в минуту.)

Применяя правила увеличения и уменьшения дробей в несколько раз, учащиеся могут решать задачи на нахождение части от дробного числа, осуществляя наглядно нахождение одной или нескольких долей от дроби.

Например, от .

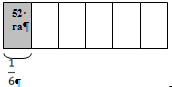
Нахождение неизвестного числа по его дроби (части), когда известно, какая именно часть дана и сколько единиц она составляет, тоже рассматривают, опираясь на наглядность, что приводит к лучшему усвоению детьми данного материала. Проиллюстрируем задачу: «В колхозе засеяно 52 га, что составляет часть всего поля. Как велика площадь поля?»

Таким образом, с введением дробных чисел в курс математики происходит расширение числовой области:

новое понятие числа требует введения нового определения понятия равенства чисел, суммы и произведения;

введение дробных чисел снимает ограничения с действия деления целых чисел (кроме деления на нуль);

дробные числа подчиняются всем законам арифметических действий, установленным для чисел натуральных.

Изучение дробных чисел в школьном курсе продолжается с появлением процента. Тему «проценты» тоже нельзя отнести к легко усеваемым. Это связано, прежде всего, с путаницей изучаемых понятий, поскольку процент представляет собой обыкновенную дробь. Ее традиционное изучение сосредоточено в строгих временных рамках курса V – VI классов, что не позволяет расширить спектр практических приложений и полноценно учитывать возрастные возможности учащихся в формировании ряда практических умений в работе с процентами.

Тема разворачивается по спирали и изучается в несколько подходов с V по IX класс включительно. При каждом проходе учащиеся возвращаются к процентам на новом уровне, их знания пополняются, добавляются новые типы задач и приемы решения. Такое многократное обращение к понятию приводит к тому, что постепенно оно усваивается прочно и осознано.

Вопросы, связанные с процентами, позволяют сделать курс практически-ориентираванным, показать учащимся, что приобретаемые ими математические знания применяются в повседневной жизни. Интерес в значительной степени поддерживается также и содержанием задач, что служит достаточно сильным мотивом для решения предлагаемых задач.

Введение процентов опирается на предметно практическую деятельность школьников, на геометрическую наглядность и геометрическое моделирование. С самого начала освоения понятия учащиеся выполняют много заданий, в которых требуется заштриховать, закрасить, начертить, вырезать часть фигуры. Широко используются рисунки и чертежи, помогающие разобраться в задаче и увидеть путь решения.

Похожие статьи:

Планирование самостоятельной работы
Основной формой обучения на заочных курсах для меня будет самостоятельная работа над учебным материалом по изучаемым предметам, с использованием методических материалов и указаний (с разбором типовых примеров, задач и упражнений по разделам математики, физики и русского языка, задания для самостоятельной работы). Решение контрольных работ с применением учебных пособий. А так же консультации с пре ...

Особенности рассказов А.П. Чехова
Творчество А.П. Чехова – творчество малого жанра. Писатель не написал ни одного романа. Что обусловило становление Чехрва именно как мастера малой формы? Этот вопрос изучали многие исследователи, среди них – А.В. Кулешов, А.П. Чудсков, М.П. Громов, Л.М. Цилкевич и многие другие. В русской литературе обстоятельства сложились так, что рассказ стал разрабатываться после того, как уже появились повес ...