Бесконечный кластер при протекании

Как растет масса, или число узлов, М(L) наибольшего кластера с увеличением характерного размера L решетки? При р>рс мы ожидаем, что m(L)≈pn(p) L2, где правая часть при L→∞ стремится к Р∞(р)L2, а Р∞(р) есть просто плотность узлов, принадлежащих перколяционному кластеру. В то же время при р<рс мы ожидаем, что т(L)/L2→ 0 при L→∞, так как Р∞(р<рс) = 0. При р=рс можно ожидать, что М(L) будет возрастать почти как L2. Экстенсивные исследования зависимости M(L) от L привели к следующему результату [4]:

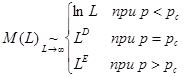(1)

Масса перколяционного кластера составляет при р>рс конечную долю всех узлов. Ниже рс кластер, простирающийся по всей решетке, как правило, не существует. Однако, если М(L) интерпретировать как размер Sмакс наибольшего кластера , то оказывается, что М(L) лишь очень слабо, т.е. логарифмически, возрастает с увеличением. На пороге протекания р=рс масса кластера, простирающегося по всей решетке (он является и наибольшим кластером), возрастает с увеличением L по степенному закону LD. Результаты численных экспериментов на квадратной решетке представлены на рис. 1.

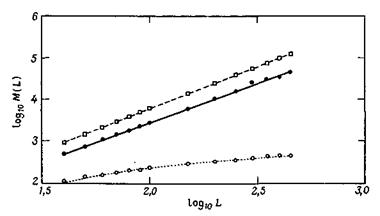
Рис. 1. Масса наибольшего кластера как функция линейного размера L квадратной решетки.

Черные кружки соответствуют р=рс=0,593. Сплошная линия-зависимость М(L)=ALD с D=1,89. При р=0,65 (светлые квадраты) кривая, проведенная через экспериментальные точки (штриховая линия), дает D = 2,03. При р = 0,5. т. е. при р < рс, экспериментальные точки (светлые кружки) ложатся на прямую M(L) = А + В In L (показанную пунктиром).

Они показывают, что перколяционный кластер на пороге протекания имеет фрактальную структуру с фрактальной размерностью D. Фрактальный перколяционный кластер на пороге протекания часто называют внутренним перколяционным кластером. Для результатов, представленных на рис. 1, фрактальная размерность D по оценкам имеет значение 1,89 + 0,03. Указанная ошибка имеет статистическую природу и характеризует качество подгонки степенного закона к результатам численного моделирования, представленным на рис. 1. Анализ систематических ошибок – дело тонкое. Когда перколяционный кластер на конечной решетке размером L составляет лишь часть внутреннего перколяционного кластера, то некоторые из узлов, не входящих в перколяционный кластер на решетке размером L, на самом деле принадлежат внутреннему перколяционному кластеру, так как соединены с ним связями, лежащими вне рассматриваемого фрагмента. При р>рс численное моделирование на квадратной решетке приводит к фрактальной размерности d= 2,03 + 0,01 для перколяционного кластеpa. И в этом случае ошибка имеет статистическую природу, a D есть угловой коэффициент прямой, проведенной через точки, полученные с помощью численного моделирования при р=0,65 и представленные на рис. 1. По точкам, соответствующим на этом рисунке наибольшим кластерам, была построена подгоночная прямая М(L) = А + В ln L с В=-426 и А = 327. Она проведена на рис. 1 штриховой линией. Все результаты численных экспериментов, представленные на рис. 1, согласуются с асимптотическим поведением, описываемым соотношением .

Похожие статьи:

Сущность гуманистического воззрения человека
Человек как самоцель развития, как критерий оценки общественного прогресса выступает поэтому как гуманистический идеал. Поступательное движение к этому идеалу связано с гуманизацией жизни общества, в центре планов и забот которого должен стоять человек со всеми своими нуждами, интересами, потребностями. Его сущность во многом определяется тем, какой системы ценностей он придерживается, что побужд ...

Место темы в базовом курсе информатики и ИКТ
Данная тема изучается в 9 или 10 классе базового курса информатики в модуле «Информационные системы и моделирование». Время изучения темы зависит от количества учебного времени отводимого на курс информатики и ИКТ в учебном плане школы. Основные цели. Сформировать предметные компетенции: 1) Уровень знаний: дать представление о способах хранения и поиска информации в базах данных, познакомить с ос ...