Мультимедийное пособие по теме «Обыкновенные дроби и проценты»

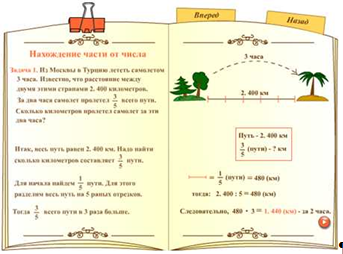
Важно сопоставить краткую запись условия с данной величиной, выраженной натуральным числом и величиной, которую надо найти. Таким образом, схематическая запись самого условия задачи, вначале этой сцены, отображается в достаточно емкую таблицу с «дано» и «найти». Процесс схематизации условия обычно вызывает затруднения у учащихся, поэтому визуализация такого процесса кажется нам весьма полезной. Следующий этап – это осознание того, на сколько равных частей разделен весь путь и сколько таких частей необходимо найти, какая дробь в итоге будет соответствовать искомому участку пути, и какой протяженностью (в км) этот участок пути окажется. Представленная модель решения такой задачи в дальнейшем переносится на класс задач типа «Отыскание части от числа (целого)».

Затем приводится алгоритм решения задач данного типа.

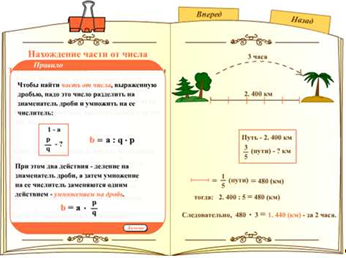
Здесь же представлено правило нахождения части от числа с помощью умножения на дробь, как обобщение выше сказанного. Формула имеет буквенную запись, обозначения компонентов в которой были введены еще в самом начале просмотра мультимедийного пособия.

Далее по кнопке перехода «Дальше» или по закладке «Вперед» попадаем в сцену «Нахождение числа по его части».

Отыскания числа (целого) по его части так же рассматривается на конкретном примере задачи. Формулировка условия задачи сопровождается динамической иллюстрацией, с переносом ключевых моментов на рисуемую картинку. Переход к подробному описанию решения осуществляется посредством кнопки «Р». После чего можно проследить логику построения разбора данного типа задачи. Каждое утверждение, размещаемое в левой части рабочего поля, подкрепляется созданием динамической картинки или выполняемым арифметическим действием в правой части визуального поля.

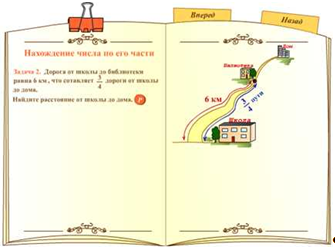
Краткая запись условия сопоставляется с данной величиной, выраженной обыкновенной дробью и величиной, которую надо найти. Таким образом, схематическая запись самого условия задачи, вначале данной сцены, отображается в достаточно емкую таблицу с «дано» и «найти». Следующий этап – это осознание того на сколько равных частей разделен путь, известный по условию задачи и сколько таких равных частей он составляет. Затем необходимо узнать какой части не хватает для отыскания всего пути (маршрута), что является связующим моментом для отображения единого алгоритма решения такого рода задач. Таким образом, представленная модель решения такой задачи в дальнейшем переносится на класс задач типа «Отыскание части от числа (целого)».

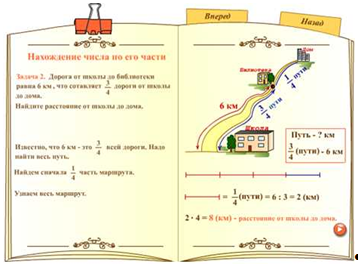
Затем приводится алгоритм решения задач данного типа.

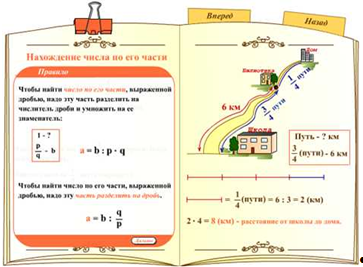
Здесь же представлено правило нахождения части от числа с помощью деления на дробь, как обобщение выше сказанного. Формула имеет буквенную запись, обозначения компонентов в которой были введены еще в самом начале просмотра мультимедийного пособия.

Серию задач продолжает задача на доли, рассмотренная в следующей сцене «Нахождение дроби, которую одно число составляет от другого».

Нахождение долей так же рассматривается на конкретном примере задачи. Формулировка условия задачи сопровождается динамической иллюстрацией, с переносом ключевых моментов на рисуемую картинку. Переход к подробному описанию решения осуществляется посредством кнопки «Р». После чего можно проследить логику построения разбора данного типа задачи. Каждое утверждение, размещаемое в левой части рабочего поля, подкрепляется созданием динамической картинки или выполняемым арифметическим действием в правой части визуального поля.

Краткая запись условия сопоставляется с данной величиной, выраженной натуральным числом и величиной, которую надо найти, в данном случае мы ищем дробь. Таким образом, схематическая запись самого условия задачи, вначале рисуемого мульта, отображается в достаточно емкую таблицу с «дано» и «найти». Следующий этап – это осознание того, на сколько равных частей разделено целое. Затем необходимо узнать какую часть составляет эта величина от целого (именно этим мы занимались, рассматривая предыдущие типы задач). Таким образом, представленная модель решения такой задачи в дальнейшем переносится на класс задач типа «Нахождение дроби, которую одно число составляет от другого». Затем приводится алгоритм решения задач данного типа.

Похожие статьи:

Оптимизация познавательной деятельности учащихся на уроках химии через игровые методы
Оптимизация- это процесс выбора наилучшего варианта из множества возможных. Автором теории оптимизации является академик Ю. К. Бабанский. Оптимизацию можно рассматривать как науку и как искусство. Как науку потому, что она требует знания и применения закономерностей, принципов, способов; может быть представлена в виде предписаний, требований, рекомендаций, общих для всех лиц, стремящихся оптимизи ...

Исторический обзор реализации интеграции в практике отечественной и зарубежной школы
Идея о единстве научных знаний, хоть и в примитивных натур-философских представлениях находила отражение в работах древних мыслителей: Аристотеля, Демокрита, Эпикура, Платона. К этой проблеме обращались Г. Гегель и И. Кант, Л. Фейербах. И.Г. Песталоцци утверждал, что процесс обучения должен быть построен таким образом, чтоб, с одной стороны, разграничить между собой отдельные предметы, а с другой ...