Дидактические материалы к урокам

После выполнения первых трех заданий, скорее всего, учащиеся смогут составить рекурсивную формулу:

, где n - количество точек.

Однако буквенную запись ученикам поможет составить учитель в ходе обсуждения гипотез групп, а сами учащиеся получат эту формулу примерно в таком виде:

Количество прямых, проведенных через n точек, никакие три из которых не лежат на одной прямой,равно количеству прямых, проведенных через n-1 точек плюс (n-1).

В качестве пропедевтики темы арифметическая прогрессия учитель может обратить внимание учеников, на то что:

=1; =1+2; и т.д.

А также, что . На плоскости n точек, никакие 3 из которых не лежат на одной прямой, каждая точка соединяется с n-1 точек n-1 отрезком, но у каждого отрезка 2 конца, поэтому количество отрезков .

Для наглядности можно привести ученикам геометрическую интерпретацию формулы 1+2+3+ +n-1=:

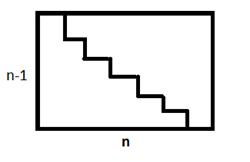
А для закрепления формулы можно дать задание посчитать на скорость:

а) 1+2+3+…+100;

б) 2+4+6+…+1000;

Далее учитель предлагает вернуться к выполнению работы. Последние 2 задачи, которые приведены в карточке, эквивалентны первоначальному заданию лабораторной работы, для их решения ученики должны воспользоваться изученной формулой.

В качестве домашнего задания учитель предлагает ученикам придумать еще несколько задач, решить которые, можно используя результаты лабораторной работы.

При подведении итогов учитель спрашивает, что на уроке ученикам показалось, трудным, а что легким, что понравилось, что не понравилось, что полезного они узнали на уроке. Ученики сдают заполненныекарточки с лабораторными работами, за выполнение которых учитель ставит оценки с учетом их работы на уроке и аккуратности построения чертежей.

Лабораторная работа №2

Тема: Формулы сокращенного умножения (7 класс).

Цели работы:

• образовательные: изучение новых знаний, формирование навыков применения формул.

• воспитательные: активизация учебной деятельности практической направленности.

• развивающие: развитие мышления и навыков счета.

Оборудование и материалы: карточки, подготовленные учителем.

План работы:

1) вводная часть;

2) вычисления;

3) решение практических задач;

4) подведение итогов урока.

Форма организации: Учащиеся решают задания индивидуально, между заданиями происходит сверка ответов и выявление ошибок.

Теоретический материал к лабораторной работе №2

В 7 классе изучаются темы «Формула разности квадратови «Квадрат суммы. Квадрат разности».

В учебнике Ш. А. Алимова кратко приведены примеры использования данных формул на практике:

1) упрощение вычислений;

2) приблизительное вычисление , при малых а;

Для лучшего запоминания формул, тренировки их применения и демонстрации их практической пользы, особенно применительно к приемам рациональных вычислений, можно провести лабораторную работу по данным темам.

Данная лабораторная работа рассчитана на целыйурок. Относительно предложенной классификации лабораторных работ данная работа относится к 3 группе (лабораторные работы, в которых требуется применить знания для решения определенной практической задачи).

Задание к лабораторной работе №2

Учитель раздает каждому учащемуся по карточке и дает указания к выполнению лабораторной работы.

Сначала на скорость вычислите выражения из первого задания. По команде учителя начинайте работу и как только закончите вычисления, поднимите руку, и учитель скажет вам время, которое вы затратили. Запишите время в соответствующую графу. Далее состоятельно выполните два задания расположенных ниже. Когда вы заполните графы с формулами приостановите работу и дождитесь остальных учеников. Используя полученные формулы, вычислите на скорость примеры из отдельной карточки выданной учителем. По команде учителя начинайте работу и как только закончите вычисления, поднимите руку, и учитель скажет вам время, которое вы затратили. Вид карточки:

Похожие статьи:

Пути и способы развития педагогических способностей
Способности – это свойства личности, которые являются условием успешного выполнения определенных видов деятельности. От природы человеку даются задатки – его личностные, характерологические, психофизиологические и другие индивидуальные особенности, которые при наличии соответствующих условий могут развиться в способности к той или иной деятельности. Черты характера, такие, как тактичность, требов ...

Использование компьютера на уроках
В настоящее время во всех школах идет раннее обучение иностранному языку. И порой недостаточно использовать традиционные средства обучения, такие как учебник, картинки и тому подобное. Поэтому все чаще учителя иностранных языков стали использовать на своих уроках компьютер. Основной причиной использования компьютерных программ можно считать то, что часто на уроках иностранного языка процесс вовле ...