Дидактические материалы к урокам

Цель игры – заполнить все клетки таблицы. Первый, кто сможет достичь цели, объявляется победителем.

После того как выявлен победитель, все рассаживаются по местам и подводятся итоги. Сначала победитель зачитывает свою карточку - как ему удалось ее собрать. После этого учитель перечисляет свойства, а ученики называют те фигуры, которые этим свойством обладают.

Учитель просит учеников сказать что им понравилось, а что нет, какие новые знания они получили (повторили).

Всем, кто смог заполнить более 85% клеток таблицы учитель может поставить пятерки, другим оценки не выставлять.

Пример карточек:

Пример заполненной карточки:

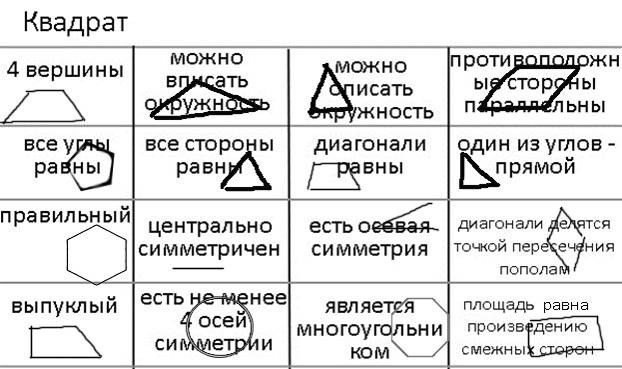
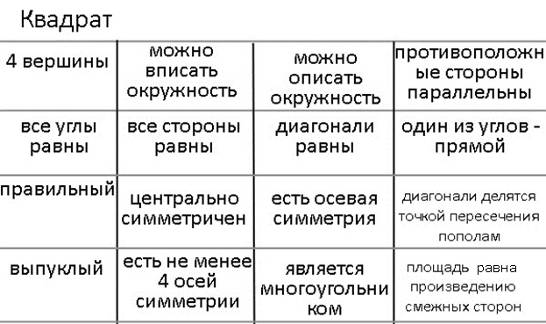
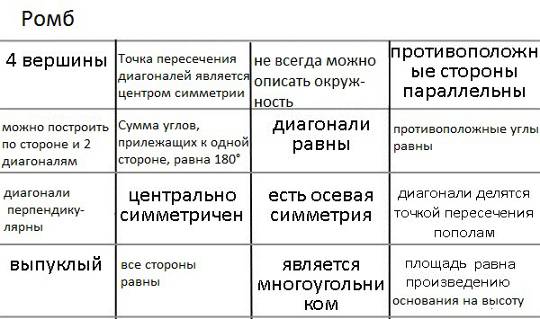
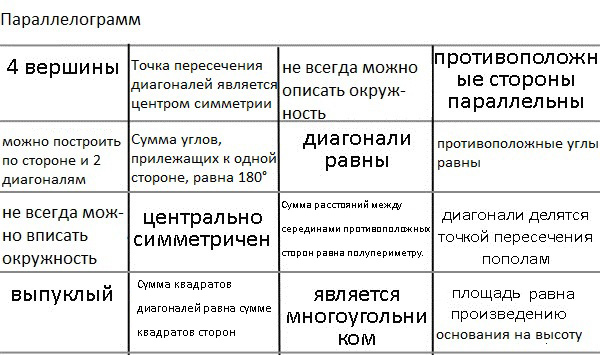
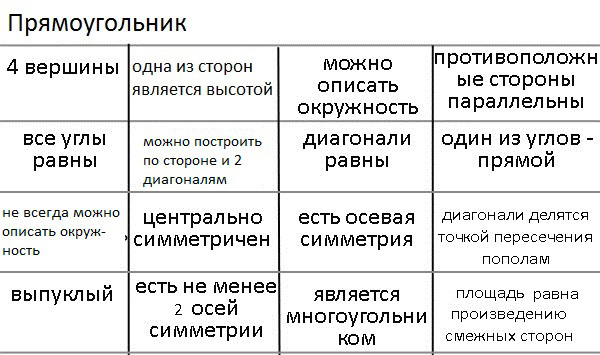
4 вершины – трапеция

все углы равны – правильный пятиугольник

правильный – правильный шестиугольник

выпуклый – прямоугольная трапеция

можно вписать окружность – треугольник

все стороны равны – правильный треугольник

центрально симметричен – отрезок

есть не менее 4 осей симметрии – окружность

можно описать окружность – равнобедренный треугольник

диагонали равны – равнобедренная трапеция

есть осевая симметрия – угол

является многоугольником – правильный восьмиугольник

противоположные стороны параллельны – параллелограмм

один из углов прямой – прямоугольный треугольник

диагонали делятся точкой пересечения пополам – ромб

площадь равна произведению смежных сторон – прямоугольник

Чтобы заполнить карточку целиком, нельзя торопиться и заполнять не анализируя. Например, в ячейку «есть не менее 4 осей симметрии» можно нарисовать окружность или правильный восьмиугольник. Однако если нарисовать в нее восьмиугольник, тогда окружность можно нарисовать только в клетки: «центрально симметричен» или «есть осевая симметрия». Рассмотрим эти случаи:

1) Окружность рисуем в ячейку «центрально симметричен», тогда отрезок можно нарисовать только в ячейку «есть осевая симметрия», но тогда некуда нарисовать угол. Значит, такой вариант не подходит.

2) Окружность рисуем в ячейку «есть осевая симметрия», но тогда некуда нарисовать угол. Значит и такой вариант не подходит. Значит клетку «есть не менее 4 осей симметрии» нужно заполнить окружностью.

Дидактическая игра №2

Тема: Область определения и область значения функции(7-11 классы).

Цели работы:

• образовательные: закрепление навыков нахождения ООФ, МЗФ и их анализа;

• воспитательные: активизация учебной деятельности;

• развивающие: развитие логического мышления.

Форма организации: Индивидуально, письменно или устно.

Теоретический материал к дидактической игре №2

Вопрос принадлежности тех или иных чисел области определения или области значения функции часто возникает при решении задач. Например, при поиске ОДЗ уравнения или неравенства. Поэтому полезны навыки анализа чисел с точки зрения принадлежности ООФ и МЗФ.

Даная игра направлена на формирование соответствующих навыков. Было сделана попытка представить задание в виде некоторого детективного сюжета, чтобы учащиеся могли почувствовать себя в роле детектива. Ученикам это может быть весьма интересно в свете популярности экранизаций Шерлока Холмса.

Игра в зависимости от количества заданий может проводиться от 10 до 25 минут.

Задание дидактической игры №2

Учитель рассказывает предысторию:

В мире функций и чисел. Последние оказываются беззащитны. Все числа поделены на сферы влияния. Каждое лежит в области определения или значения какой-либо функции. И функции воздействуют на числа, изменяя их до неузнаваемости. Не раз бывало, что просыпаясь утром двойкой, число, попав под горячую руку у=х2,оказывалось четверкой.

Но однажды был принят закон, запрещающий функциям воздействовать на числа. Представьте, что вы работаете детективами в этом мире. Поступило сообщение, о нарушении закона. Вы прибыли на место преступления и увидели следующую картину:

1) Были задержаны трое подозреваемых: , у= и y=x.

Похожие статьи:

Методические рекомендации к использованию пособия
Значительная роль в образовании, развитии, подготовке учащихся к труду и их социальной адаптации принадлежит усвоению математических понятий, в частности обыкновенных дробей и процентов. Получая знания об обыкновенных дробях и процентах, школьники расширяют свои представления о числе и границе вычислительных возможностей. На примере изучения дробей они узнают то общее, что свойственно всем числам ...

Описание методики работы по воспитанию наблюдательности у детей в процессе ознакомления с комнатными растениями
Ко времени прихода детей в детский сад воспитатель должен позаботиться о том, чтобы в группе находились цветущие комнатные растения, а также яркие красивые леечки без ситечек. Воспитывая у детей интерес к таинственному миру растений, дети знакомятся с конкретными видами комнатных растений, узнают их названия, характерные особенности. Узнают, что они живые существа и у них есть потребности в опред ...