Методика изучения геометрических величин. Теория измерения длин отрезков

Разделив почленно на S, получаем:

m/n<=S1/S<=m/n +1/n

в) Отношение АВ1/АВ и S1/S удовлетворяют одним и тем же неравенствам, причем числа m/n и m/n+ 1/n отличаются на величину 1\n. При сколь угодно больших n значение 1/n становится очень малым, а это возможно только тогда, когда числа равны. Итак:

S1/S=AB1/AB, ч. т. д.

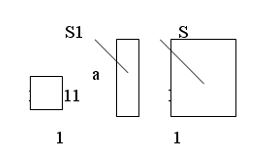
Для вывода формулы площади прямоугольника воспользуемся только что доказанным свойством по отношению к квадрату, со стороной 1 и прямоугольником со сторонами 1 и а и а и в. Получаем:

S1/1=a/1; S/S1=в/1 => S1=а, S=S1в.

Следовательно:

S=а*в.

VII.Площади подобных фигур.

Площади подобных фигур относятся как квадраты их соответствующих линейных размеров.

При доказательстве этого утверждения используют понятие простой фигуры, определение подобных фигур. Если фигура разбивается на простые треугольники, площади которых обозначим через , а фигура - на треугольники, площади которых и фигуры и подобны с коэффициентом , то линейные размеры треугольников в раз изменены, по отношению к размерам треугольников , то: и т. д., поэтому:

VIII. Площадь круга.

Круг – плоская фигура, но ее нельзя разбить на простые треугольники. Поэтому, такая фигура имеет площадь , если существуют содержащие её простые фигуры и содержащиеся в ней простые фигуры с площадями, как угодно мало отличающимися от .

При проведении уроков по теме «Площадь фигур» вывод общих формул должен закрепляться на частных примерах. Изложение теоретического материала должно быть максимально сокращено (в разумных пределах), что позволило бы сэкономить время для решения более сложных задач. (Возможно проведение уроков-лекций для изложения теории). Желательно проводить самостоятельные работы, как обучающего, так и контролирующего характера по каждому из изучаемых случаев.

Задача 1.

а) Разделите данный треугольник на три равновеликие части прямыми, проходящими через одну вершину.

B

A B1 D B2 C

б) Разделите данный параллелограмм на три равновеликие части прямыми, проходящими через одну вершину.

B C

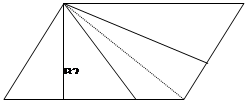
A K B1 D

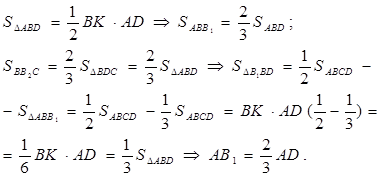
Аналогично: Поэтому точки и делят соответственно отрезки и в отношении 2:1 от вершин и соответственно.

Похожие статьи:

Диктант как метод формирования орфографической зоркости
Орфографическая зоркость – способность пишущего видеть орфограммы в тексте. Ее не следует смешивать со зрительной памятью и зрительным восприятием. Умение видеть орфограммы достигается долгой тренировкой. Развитию орфографической зоркости способствуют диктанты. Диктант – это один из видов письменных работ для закрепления и проверки знаний, тренировки навыков учащихся; наибольшее распространение п ...

Техническая конференция
Во внеклассной работе по технологии уделяется внимание такой форме проведения массового внеклассного мероприятия как техническая конференция. Конференция - форма организации научной деятельности, при которой исследователи (не обязательно учёные или студенты) представляют и обсуждают свои работы. Цель проведения технической конференции в школе – популяризация новейших достижений техники, производс ...