Методика изучения геометрических величин. Теория измерения длин отрезков

.

Принципиальным моментом в теории объемов тел является обоснование формулы для учащихся является достаточно трудным и сложным. Структурная сложность доказательства подсказывает, что при его изучении целесообразно воспользоваться приёмами выделения логической структуры доказательства (разбиения доказательства на отдельные шаги, составление логико-структурной схемы доказательства и т.д.). Наличие в доказательстве трудных для понимания рассуждений говорит о целесообразности использования приёмов конкретизации, моделирования и т.д.

Структура доказательства формулы объёма прямоугольного параллелепипеда:

1. устанавливается величина отношения высот двух параллелепипедов с общим основанием;

2. устанавливается величина отношения объёмов выбранных параллелепипедов;

3. сравнение полученных значений отношений;

4. вывод формулы объёма прямоугольного параллелепипеда, применяя доказанное свойство к единичному кубу и параллелепипедам с измерениями: a,1,1; a,b,1; a,b,c.

При решении задач учащиеся иногда “путают” свойства прямого и прямоугольного параллелепипедов, неправильно указывают их диагональное сечение и т.п. Более углубленное изучение этих понятий на этапе их введения обеспечивает применявшаяся ранее методическая схема:

1. проанализировать эмпирический материал;

2. математизировать эмпирический материал – построить определение;

3. составить алгоритм распознавания понятия;

4. включить понятие в систему понятий.

Задача № 5.

Грани параллелепипеда – равные ромбы со стороной а и острым углом 600. Найдите объем параллелепипеда.

.

∆ AA1O: ; Из ∆ AA1K: .

Из ∆ AOK: ; Из ∆ AA1O: ;

Из ∆ KA1O:

.

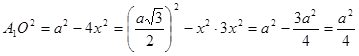
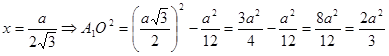
Ответ: .

Построение строгой теории измерения геометрической величины в школьном обучении наталкивается на серьезные трудности. Это не означает отказа в школьном курсе от всякой теории измерения геометрических величин. Главное – стремление к строгости не должно быть самоцелью, но не следует скрывать от учащихся вынужденных логических пробелов. Например, площадь многоугольника определяется как сумма площадей треугольников, на которые его можно разбить. Естественно возникает вопрос, получим ли то же самое число, если разобьем данный многоугольник на треугольники другим способом и сложим площади треугольников разбиения. В школе не изучается теорема о независимости суммы площадей треугольников разбиения от способа разбиения, но об её существовании следует сообщить учащимся о существовании такого факта.

Похожие статьи:

Организация и методика исследования
Эксперимент проводился в Красноярской специальной (коррекционной) общеобразовательной школе-интернате VIII вида №6. В 2007-2008 году школа работает в режиме шестидневной недели, в одну смену. Каждому учителю, работающему в школе предоставлено право на творческое самовыражение, выбор форм и методов обучения и воспитание детей. Цель нашего исследования - экспериментально проверить эффективность при ...

Работа с родителями
Мировая статистика убеждает, что современное семейное воспитание не столь эффективно, полноценно, как должно быть. Психолого педагогическое просвещение родителей, осуществляемое дошкольным учреждением имеет целевую направленность. Критериями эффективности работы по включению родителей в деятельность дошкольного учреждения являются: - повышение уровня педагогической культуры родителей; - посещение ...