Методика изучения геометрических величин. Теория измерения длин отрезков

Задача 2.

Докажите, что стороны треугольника обратно пропорциональны его высотам, то есть:

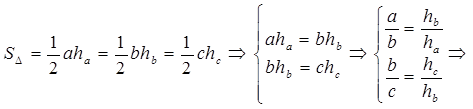
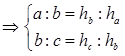. Так как 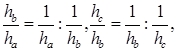получаем:

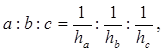что требовалось доказать.

Задача 3.

Докажите, что среди всех параллелограммов с данными диагоналями наибольшую площадь имеет ромб.

M B C

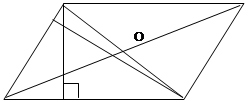
A K D

1-ый способ

.

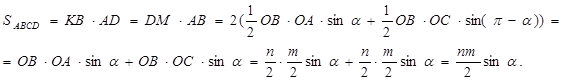
Если - ромб, то , то есть 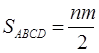. Наибольшее значение произведения зависит от наибольшего значения , которое достигается при , если , то . Следовательно, площадь ромба наибольшая среди всех площадей параллелограммов с данными диагоналями.

2-ой способ

.

Составим функцию, выражающую площадь параллелограмма:

при .

Так как - наименьший угол, образуемый диагоналями при пересечении, то и будет точкой максимума, следовательно: ; и этот параллелограмм – ромб.

Задача 4.

Прямая, перпендикулярная высоте треугольника, делит его площадь пополам. Найдите расстояние от этой прямой до вершины треугольника, из которой проведена высота, если она равна .

B

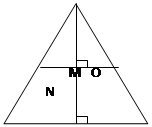
A D C

- трапеция, то есть подобен

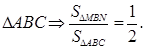
Так как для подобных треугольников их площади относятся как квадраты соответствующих линейных размеров, то:

Существуют различные методические подходы к изучению вопросов измерения геометрических величин в курсе стереометрии.

Для вывода формулы объема, могут быть использованы:

1. Принцип Кавальери: объемы (или площади) двух тел (фигур) равны, если равны между собой площади (длины) соответствующих сечений, проведенных параллельно некоторой данной плоскости (прямой).

2. Формула Симпсона:

.

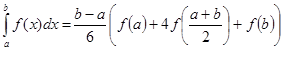Пусть промежуток [a,b] разбит на n частейных промежутков [xi, xi+1] длины , при этом n считается чётным числом, и для вычисления интеграла по промежутку [x2k, x2k+2] используется приведенная формула:

Похожие статьи:

Модель рефлексии в педагогической деятельности
В области педагогики слово «модель» означает образ, стандарт, на который ориентируются ученые и практики в преобразовании педагогической действительности; мера изменений педагогической действительности с уточнением границ и условий; способ педагогического исследования, используемый для развития идеи о согласованности различных элементов педагогического объекта. Модель выступает как промежуточное ...

Сущность понятий «дидактическое обеспечение» и «дидактические средства»
Под дидактическим обеспечением понимается комплекс взаимосвязанных по дидактическим целям и задачам образования и воспитания разнообразных видов содержательной учебной информации на различных носителях, разработанный с учетом требований психологии, педагогики, валеологии, информатики и других наук, и используемый для дистанционного образования. Дидактическое обеспечение оценивается по следующим п ...