Методические разработки занятий факультативного курса

2. Решение систем уравнений

Теперь мы можем применять знания о симметрических многочленах при решении систем уравнений с 2-мя неизвестными.

Пример 1. Решить систему:

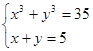(1)

Введем новые переменные

σ1 = x + y и σ2 =xy;

x3 + y3 = s3 = σ13 - 3 σ1 σ2

Для новых переменных получаем следующую систему:

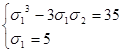(2)

Подставляя значение σ1 = 5 в первое уравнение системы (2) получаем :

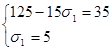
Решение системы (2) таково: σ1 = 5 , σ2 = 6. Вернемся к переменным x и

y:

Выражая из 1-го уравнения y и подставляя во второе, приходим к

Решая 2-е уравнение, находим х = 2 или х =3. Подставляя эти значения в первое уравнение, получаем решения исходной системы (1): (2,3) или (3,2).

Ответ: (2,3) или (3,2).

Пример 2. Решить систему

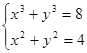(1)

Как и в предыдущем примере, произведем замены σ1= x + y и σ2 =xy, тогда x3 + y3 = s3 = σ13 - 3 σ1 σ2 и x2 + y2 = σ12 - 2 σ2 .Перейдем к системе с другими переменными:

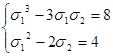
Выражая из 2-го уравнения σ2 = 1/2 σ12 – 2 и подставляя в 1-е, получаем

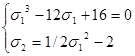(2)

Первое уравнение данной системы – кубическое. Попытка угадать корень дает результат, σ1 = 2 – подходит. Если мы разделим σ13 - 12 σ1 + 16 на σ1 – 2, то получим многочлен уже 2-й степени и сможем решить нужное нам уравнение.

Задание: Разделить

σ13 - 12 σ1 + 16 на σ1 – 2.

Ответ: σ12 + 2 σ1 – 8Итак, по следствию из теоремы Безу имеем:

σ13 - 12 σ1 + 16 = 0, или

(σ1 – 2)( σ12 + 2 σ1 – 8) = 0,Откуда σ1 = 2 или σ1 = -4.

Подставляя эти значения во 2-е уравнение системы(2), получаем:

σ1 = 2; σ2 = 0 или σ1 = -4 ; σ2 = 6 .Возвращаемся к x и y :

или

Вторая система решения не имеет, а из первой находим

Ответ: (2,0) или (0,2).

ЗАДАНИЕ: Решить системы уравнений:

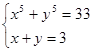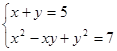1. 2. 3.

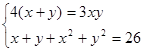
Ответы:1. Вспомогательная система имеет решения σ1 = 3, σ2 = 2 или σ1 = 3, σ2 = 7 Окончательный ответ: (2,1) или (1,2).2. Вспомогательная система имеет решения σ1 = 5, σ2 = 6 Окончательный ответ: (2,3) или (3,2)3. Вспомогательная система имеет решения σ1 = 6, σ2 = 8 или σ1 = -13/3, σ2 = -52/9

Окончательный ответ: (2,4) или (4,2) или (, ) или (, )

Домашнее задание

Решить системы уравнений:

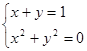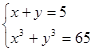1. 2. 3.

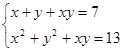
Ответы:

1. Вспомогательная система имеет решения σ1 = 1, σ2 =1/2 Окончательный ответ: корней нет

Похожие статьи:

Особенности формирования технике чтения на начальном этапе обучения
Одним из возможных эффективных путей повышения качества преподавания иностранного языка в начальной школе является разработка таких учебных материалов, которые соответствуют возрастным особенностям и познавательным интересам детей младшего возраста (Ш.А. Амонашвили, Б.В. Беляев, Л.И. Божович, Л.С. Выготский, В.В. Давыдов, В.А. Крутецкий, А.А. Леонтьев, И.А. Мещерова, В.М. Филатов). Авторы методик ...

Роль классного руководителя по организации внеклассных мероприятий с учащимися 5-го класса
Роль классного руководителя в системе образования очень велика, т.к. порой ученики обращаются к классному руководителю с вопросами сложными и неприятными, связанными с парадоксами нашей действительности. Классный руководитель должен, во-первых, не уходить от ответа и, во-вторых, искать его вместе. Ему очень важно чутко улавливать настроения в среде школьников, не стремиться сразу, осудить все или ...