Методические разработки занятий факультативного курса
2. Вспомогательная система имеет решения σ1 = 5, σ2 = 4 Окончательный ответ: (1,4) или (4,1)
3. Вспомогательная система имеет решения σ1 = 4, σ2 = 3 или σ1 = -5, σ2 = 12 Окончательный ответ: (1,3) или (3,1)
Занятие 4
Цель: Научить детей находить подходящие замены для приведения уравнений и систем уравнений к симметрическому виду, и решать такие уравнения и системы.
План занятия:1. Введение вспомогательных неизвестных для приведения систем уравнений к симметрическому виду.2. Введение вспомогательных неизвестных для решения уравнений.3. Домашнее задание.
Приведение систем уравнений к симметрическому виду
На предыдущем занятии мы с вами решали симметрические системы уравнений. А что делать, если система не является симметрической, но очень на нее похожа? Сделать замену переменных так, чтобы система стала симметрической.
Пример 1:
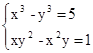
Эта система не является симметрической, но если произвести замену z = -y, то она станет таковой
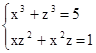
Пример 2. Привести систему к симметрическому виду:
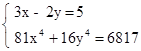
В данном случае замена не так очевидна. Нужно заметить, что 81x4 = (3x)4, и16y4 = (-2y)4. Заменяя 3x на u, -2y на v, получаем нужную систему:
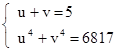
Задание. Привести системы к симметрическому виду:
1. 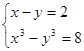 2.
2. 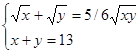 3.
3. 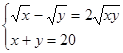 4.
4. 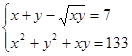
5. 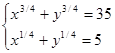 6.
6. 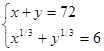
Ответы:
1. y = -z
2. ![]() = u,
= u, ![]() = v
= v
3. ![]() = u,
= u, ![]() = -v
= -v
4. ![]() = u,
= u, ![]() = v
= v
5. x1/4 = u, y1/5 = v
6. x1/3 = u, y1/3 = v
2. Решение уравнений
Иногда введением вспомогательных неизвестных можно решать достаточно сложные уравнения с одной переменной, сведя его к симметрической системе с 2-мя неизвестными.
Пример 1. Решить иррациональное уравнение:
![]() +
+ ![]() = 5
= 5
Решение
Положим ![]() = y и
= y и ![]() = z, тогда рассматриваемое уравнение примет вид y + z = 5. Кроме того, x4 + z4 = x + (97 - x) = 97. Таким образом, мы получили систему уравнений
= z, тогда рассматриваемое уравнение примет вид y + z = 5. Кроме того, x4 + z4 = x + (97 - x) = 97. Таким образом, мы получили систему уравнений 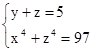 Эта система уравнений – симметрическая, делаем стандартную замену σ1 = y + z, σ2 = yz, приходим к системе
Эта система уравнений – симметрическая, делаем стандартную замену σ1 = y + z, σ2 = yz, приходим к системе 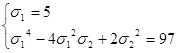 Решая ее, и возвращаясь к y и z, получаем:
Решая ее, и возвращаясь к y и z, получаем:
y + z = 5, yz =6 или y + z = 5, yz = 44Вторая система не дает решений, а из первой получаем
y = 2, z = 3 или y = 3 , z = 2, откуда уже можно найти Ответ: x = 16 или x = 81.
Пример 2. Свести уравнение к решению симметрической системы и решить его:
![]()
![]()
Похожие статьи:
Выводы по результатам проведенной коррекционно-развивающей работы
С целью выявления результативности коррекционно-развивающей работы была проведена повторная диагностика изучения индивидуальных особенностей мышления детей с диагнозом умственная отсталость с опорой на батарею тестов Л.Ф. Тихомировой: 1.Тест «Классификация предметов»; 2.Тест «Сравнение предметов»; 3.Тест «Выделение существенных признаков»; 4.Тест «Аналогии»; 5.Тест «Обобщение»; Изучение эмоционал ...
Формирование интонационной выразительности речи
1. Развитие восприятия различных видов интонации. Логопедическая работа проводится в определенной последовательности: 1. Общее знакомство с интонацией и средствами ее выражения (темп, ритм, высота и тон голоса, логическое ударение). 2. Развитие восприятия интонации повествовательного типа: а) знакомство с повествовательной интонацией; б) определение картинки-символа; в) упражнения по выделению по ...

