Методические разработки занятий факультативного курса
Пример 2. Составить квадратное уравнение, корнями которого являются числа 
, 
,где x1 , x2 – корни квадратного уравнения 
Решение: по формулам Виета для уравнения имеем 
и 
По тем же формулам для искомого уравнения: 
После раскрытия скобок ясно, что p и q – симметрические многочлены, их можно выразить через степенные суммы, затем через 
= 1 и 
= -3, после чего найдем p и q.
Проделаем это:
Таким образом, p = - 140 , q = - 833 , и поэтому искомое квадратное уравнение имеет вид: 
Задания:1. Составить квадратное уравнение, корнями которого являются кубы корней квадратного уравнения 
2. Составить квадратное уравнение с корнями 
, 
, если известно, что 
и + = 13. Доказать, что если , - корни квадратного уравнения 
с целыми коэффициентами p и q , то при любом натуральном n число 
является целым.
Ответы:
1. 
2. Пусть искомое уравнение имеет вид , тогда 
и 
. Заданные соотношения и + = 1 перепишем в виде системы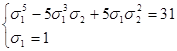 
, или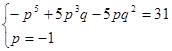 
Подставив значение p в 1-е уравнение, получим 2 решения q = 3, q = -2Ответ: 
или 
3. Вспомним формулу sk = σ1sk-1 - σ2sk-2. У нас 
, 
,и формула перепишется в виде 
(*)Доказательство проведем по индукции:
Похожие статьи:
Решение дидактических задач при помощи информационных технологий
Таким образом, используя информационные технологии, можно, интегрируя их в учебный процесс, более эффективно решать целый ряд дидактических задач на уроке на старшем этапе обучения: ― формировать навыки и умения чтения, непосредственно используя материалы сети разной степени сложности; ― совершенствовать умения аудирования на основе аутентичных звуковых текстов сети Интернет, также со ...
Виды игр в педагогической системе
По форме деятельности игры можно разделить на индивидуальные, парные, групповые, общеклассные. По образовательным задачам на игры, изучающие новый материал, формирующие умения и навыки, много игр обобщающего характера, повторения и контроля знаний. По типам: познавательные, ролевые, деловые, комплексные. По форме проведения: игры – аукционы, защиты. Путешествие по станциям, пресс – конференции, и ...