Методические разработки занятий факультативного курса

Ответ выглядит так:

.

2. Разложение симметрических многочленов на множители методом неопределенных коэффициентов

Если при выражении симметрического многочлена через и получается многочлен 2-й степени относительно , который корней не имеет, то может помочь другой способ. Многочлен от x и y 4-й степени представляется в виде произведения двух многочленов второй степени, имеющих специальный вид: , где А, В и С – какие-то пока неизвестные (или «неопределенные») коэффициенты. Как найти эти коэффициенты, мы узнаем из примера 2:

Пример 2. Разложить на множители многочлен

Решение: Мы будем искать разложение в виде

=(*)

При нахождении коэффициентов А, В и С заметим, что равенство (*) должно представлять собой тождество, то есть выполняться при любых значениях переменных x и y. Подставляя в соотношение (*) различные значения x и y, мы будем получать уравнения на коэффициенты А, В и С, после чего сможем найти их.

Положим x = y = 1, тогда (*) примет вид 16 = (А + В + С)2, откудаА + В + С = 4. Поскольку при значении 4 и -4 правая часть равенства (*) не меняется, для простоты возьмем А + В + С = 4.

Полагая x = 1, y = -1, получим А - В + С = 2,и при x = 0, y = 1, получается АС = 2.

Мы пришли к системе 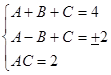.Решая ее, находим А = 1, В = 1, С = 2 (или А = 2, В = 1, С = 1).И в одном, и в другом случае ответ таков: Это равенство получено в предположении, что искомое разложение (*) существует. Раскрыв скобки в правой части, можно убедиться в справедливости полученного равенства.

3. Домашнее задание

Разложить на множители следующие многочлены:

1.

2.

3.

Ответы:

1.

2.

3.

Занятие 9

Цель: Научить детей решать некоторые задачи, не вошедшие в предыдущие занятия.

План: 1. Разбор некоторых задач. 2. Упражнения.

1. Различные задачи

Симметрические многочлены можно применять и для решения задач многих других видов, отличающихся от рассмотренных ранее.

Пример 1. Исключить x и y из уравнений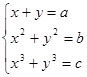

Эту задачу следует понимать следующим образом: так как для двух неизвестных x и y мы имеем три уравнения, то эта система имеет решения не при любых значениях a, b и c. Требуется найти соотношение между a, b и c, при котором данная система разрешима.

Решение: воспользуемся тем, что левые части уравнения симметрично зависят от x и y. Выразим их через элементарные симметрические многочлены: 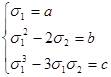Из первых двух уравнений получаем: , , и в силу третьего уравнения , или . Это и есть результат исключения x и y из исходной системы уравнений.

Похожие статьи:

Особенности внимания заикающихся дошкольников
В последнее время логопеды все больше убеждаются, что при устранении заикания невозможно обойтись без использования психологических методов воздействия. Почему же успешное логопедическое воздействие невозможно без параллельного проведения коррекционной работы по развитию психических процессов? Дело в том, что возникшие у ребенка речевые запинки, спотыкания (несудорожного или судорожного характера ...

Формирование просодического компонента в речи детей с ЗПР средствами театрализованной игры
В формировании просодического компонента речи отчетливо выступает связь речевого и умственного развития детей, развития их мышления, восприятия, наблюдательности, эмоциональности. Чтобы интересно, эмоционально и ритмически грамотно рассказать о чем-нибудь, нужно ясно представлять себе объект рассказа (предмет, событие), уметь анализировать предмет, отбирать основные (для данной ситуации общения) ...