Методические разработки занятий факультативного курса

База: - целое число, - тоже целое число.Индуктивное предположение: если и - целые числа, то - тоже целое число.Справедливость индуктивного предположения очевидна, если принять во внимание формулу (*). Итак, доказательство закончено.

Домашнее задание

1. Пусть и - корни квадратного уравнения . Вычислить значение выражения при n = 1, 2, 3, 4, 5.2. При каком действительном а сумма квадратов корней уравнения принимает наименьшее значение?

Ответы:

1.

2. Сумма квадратов корней имеет вид (а - 1)2 + 5 Наименьшее значение получается при а = 1.

Занятие 6

Цели: Научить детей доказывать справедливость неравенств, опираясь на свойства симметрических многочленов.

План:

1. Повторение.

2. Теорема 2.

3. Доказательство неравенств.

4. домашнее задание.

1. Повторение

Разбор примеров домашнего задания.

Повторение: теорема 1.

2. Теорема 2

С помощью симметрических многочленов можно доказывать различные неравенства. Но для этого нам понадобится следующая

Теорема 2. Пусть и - действительные числа. Для того, чтобы оба числа x , y, определяемые из системы уравнений 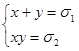,были действительными и неотрицательные, необходимо и достаточно, чтобы и удовлетворяли неравенствам , , .

Вышеприведенная теорема применяется для доказательства неравенств следующим образом: пусть дан некоторый симметрический многочлен и требуется доказать, что при всех действительных значениях x и y должно выполняться a. Для доказательства мы прежде всего будем заменять симметрический многочлен на его выражение через и . Затем, в зависимости от условия задачи, в полученном многочлене возможно два вида замены: 1) Заменить на его выражение через и неотрицательную величину , то есть подставить .2) Заменить его выражением через и z, то есть .

Похожие статьи:

Опыт практической работы по воспитанию наблюдательности у детей в процессе ознакомления с комнатными растениями
Для выяснения возможностей воспитания наблюдательности у детей в процессе ознакомления с комнатными растениями, мы обратились в один из детских садов г.Читы, а именно №22, для более близкого знакомства с опытом работы воспитателей в данной сфере. Мы познакомились с воспитателем подготовительной группы Макаровой Н,М., которая проводит подобную работу с детьми в своей группе №3. Мы изучили данный п ...

Формирование ценностного отношения к профессиональной деятельности у будущих учителей
Учитывая результаты диагностических исследований, полученных на констатирующем этапе эксперимента, были внесены изменения в условия формирования ценностного отношения к профессиональной деятельности у студентов колледжа, будущих учителей, входящих в состав экспериментальной группы. В целях оптимизации процесса формирования у студентов, будущих учителей, ценностного отношения к профессиональной де ...