Методические разработки занятий факультативного курса

Вторая система решений не дает, а из первой получаем ответ:(,) или (,)

Занятие 5

Цели: Научить детей решать задачи, в которых требуется вычислить некоторые выражения, содержащие корни заданного квадратного уравнения.

План: 1. Повторение.

2. Теорема 1.

3. Задачи о квадратных уравнениях. 4. Домашнее задание.

1. Повторение.

Существует тип задач, где по исходным данным некоторого квадратного уравнения (корням или коэффициентам) надо составить какое-нибудь выражение или другое квадратное уравнение. Задачи такого типа достаточно сложны, и применение свойств симметрических многочленов существенно упрощает их решение.

Перед разбором примеров хорошо бы вспомнить:- Формулы Виета ( , )- Степенные суммы высоких порядков s5 = σ15 - 5 σ13 σ2 + 5 σ1 σ22 s6 = σ16 - 6 σ14 σ2 + 9 σ12 σ22 - 2 σ23

Теорема 1.

- В дальнейшем мы будем использовать следующую теорему:

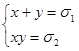Теорема 1. Пусть и - два произвольных числа. Квадратное уравнение (*) и система уравнений (**)связаны между собой следующим образом: если и - решения уравнения (*), то система (**) имеет 2 решения: 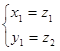, 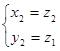и других решений не имеет; и обратно, если x = a, y = b – решения системы (**) , то числа a и b являются корнями квадратного уравнения (*).

Доказательство приведено в приложении.

Мы будем использовать теорему 1 на следующем занятии, а сейчас займемся квадратными уравнениями.

Задачи о квадратных уравнениях

Пример 1. Дано квадратное уравнение . Нужно составить новое квадратное уравнение, корнями которого являются квадраты корней данного уравнения.

Для решения этой задачи обозначим корни данного уравнения через и , корни искомого – через и , а коэффициенты искомого уравнения – через p и q. Тогда по теореме Виета , - это для корней исходного уравнения, а для искомого должно быть и . По условию задачи и , поэтому Зная коэффициенты искомого квадратного уравнения, запишем ответ:

Похожие статьи:

Исторический анализ проблемы преподавания психологии в школе
Методика преподавания психологии во многих странах находится только в начальном периоде своего становления, несмотря на то, что само преподавание психологии имеет столь же долгую историю, как и сама психология. Работы по методике преподавания психологии публиковались на протяжении всего XX в., но появлялись они достаточно редко и касались лишь отдельных аспектов данной сферы деятельности. История ...

Особенности построения и проведения интегрированных уроков
Организация учебно-воспитательного процесса в новых инновационных технологиях требует от современного учителя совершенствования практической деятельности путём поиска новых ценностных приоритетов в определении целей и содержания, форм и методов построения учебной деятельности учащихся. Одно из направлений методического обновления уроков в начальных классах – конструирование интегрированных уроков ...