Методические разработки занятий факультативного курса

Решение

Сделаем замену = u, = v, откуда u + v = 2.Кроме того, u3 + v3 = 1 + + 1 - , и получаем u3 + v3 = 2.

Решая систему 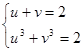, приходим к решению u = v = 1.

Вспомним, что u = , и получим

Ответ: x = 0.

Задания Найти замену, сводящую уравнения к решению симметрической системы:

1.

2.

3.

4.

5.

Ответы

1. z2 + 1 = u, z2 - 1 = v 2. , 3.

и система примет вид 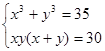4. , 5. Перенесем второй корень в правую часть и возведем обе части уравнения в 4-ю степень: . Теперь уже можно получить симметричную систему, сделав замену ,

3. Домашнее задание

Решить уравнения и системы уравнений:

1.

2.

3.

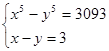
4.

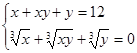
Ответы:

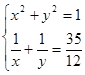1. Замена . Система примет вид . Учитывая равенство, приходим к вспомогательной системе .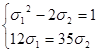

Ее решения: 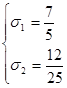или .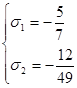

Отсюда можно найти 4 решения симметрической системы, но условию у 0 удовлетворяют лишь 3 из них: , , .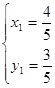

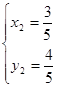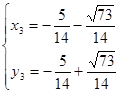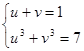Решения исходного уравнения: 4/5 , 3/5 , - 5/14 - /14.2. Заменяя , , получим систему: , вспомогательная система 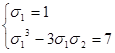имеет единственное решение , . Ему соответствуют 2 решения симметрической системы: 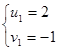, 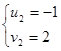. Поскольку , то исходное уравнение имеет 2 решения: 2 и 11. 3. Подстановка y = -z приводит систему к симметричному виду: 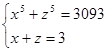Вспомогательная система: 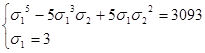Ее решения: 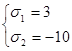, 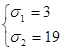Решения симметрической системы: 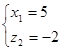, 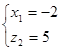И, наконец, ответ: (5,2) или (-2,-5)4. Подстановка: , Симметрическая система: 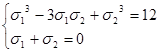Выразив из второго уравнения и подставляя в первое, получим , откуда решениями вспомогательной системы будут ,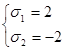

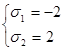
Похожие статьи:

Протекание
Бродбент и Хаммерсли рассмотрели общую ситуацию, возникающую при случайном распространении жидкости через среду, когда абстрактные термины "жидкость" и "среда" могут быть интерпретированы в соответствии с физическим смыслом задачи. В обычных процессах диффузии случайность есть не что иное, как случайные блуждания частиц жидкости. Примером могут служить нерегулярное тепловое дв ...

Особенности проведения занятий по формированию просодического компонента речи у детей с ЗПР
В учебном плане дошкольного учреждения для детей ЗПР предусмотрено к формированию связной речи в старшем подготовительном возрасте 2 занятия в неделю. Наряду с “Программно-методическим оснащением коррекционно-развивающего воспитания и обучения дошкольников с ЗПР” под редакцией С.Г. Шевченко используется дополнительная литература: Е.Д. Худенко,С.Н. Шаховская, Г.А. Ткаченко “Планы-конспекты логопед ...